Transmissionsrækkevide

CCTV-overvågningssystemer kræver ofte lange strømforsyningskabler for at levere de tilsluttede elektroniske enheder, f.eks. kameraerne. Derfor skal et "spændingsfald" ved strømforsyningskablet, som er en nøgleparameter - overvejes. I mange tilfælde er installatørerne ikke opmærksomme på virkningerne af strømmen gennem strømforsyningskablerne, mens strømforsyningen er et centralt spørgsmål ved design af CCTV systemer.

Producenterne giver ofte en specifik forsyningsspænding, f.eks. 12 VDC til deres enheder uden det tilladte interval (minimum og maksimum spænding). De praktiske tests viser, at for et 12 V-kamera kan spændingen falde til 11 V. Under denne værdi kan der være interferenser og tab af videosignal. Spændingsfaldet på kablet mellem strømforsyningen og kameraet må ikke overstige 1 V. Mange kunder bruger forskellige strømforsyningsregnemaskiner uden nogen teoretisk og praktisk baggrund, så vi diskuterer dem i denne artikel.

Den elektriske modstand af ethvert kabel er større end 0. To effekter kan observeres, når strømmen strømmer gennem kablet med en vis modstand.

1. Spændingen falder i overensstemmelse med Ohms lov.

2. Den elektriske energi omdannes til termisk energi i overensstemmelse med Ohms lov.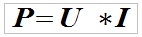

eller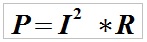

Hver ledninger er modstande. Nedenfor er et erstatningsdiagram for et tolederkabel (inklusiv modstand).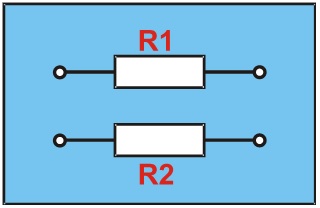

Der skal tillades spændingsfald i begge kerner; således er den samlede modstand (R) for tolederkablet R = R1 + R2.

Et kredsløbsdiagram over et spændingsfald i tolederkabel: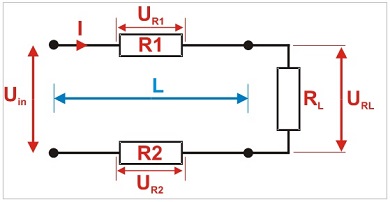

hvor:
U_i - forsyningsspænding, f.eks. fra strømforsyningen
I - strøm i kredsløbet,
R1 - modstand på tværs af det første kabelled,
R2 - modstand af det andet kabelled,
U_R1 - spændingsfald på det første kabelled,
U_R2 - spændingsfald af det andet kabelled,
L - kabellængde,
R_L - belastning, f.eks. kamera,
U_RL - spænding ved belastningen.

Efter at have leveret spændingen fra strømforsyningen (U_in) til kablet og tilsluttet belastningen (R_L), strømmen (I) strømmer gennem kredsløbet, hvilket resulterer i et spændingsfald (U_R1 + U_R2) på tværs af kablet. Forholdet er som følger: udgangsspændingen ved belastningen reduceres med spændingsfaldet på kablet.

Spændingsfaldet (Ud) beregnes ved hjælp af følgende formel for konstant og vekslende (enfaset) spænding: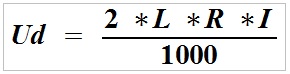

hvor:
Ud - spændingsfald målt i volt (V),
2 - konstant antal som følge af det faktum, at vi beregner spændingsfaldet for to kabler,
L - kabellængde udtrykt i meter (m),
R - modstand af et enkelt leder udtrykt i ohm pr. kilometer (Ω/km),
I - strøm forbrugt af belastningen udtrykt i ampere (A).

Spændingsfald afhænger ikke af indgangsspændingen, men af ​​ strømindgangen, lederlængde og modstand .

Langt størstedelen af CCTV-kameraer har en variabel strømindgang. Den aktuelle indgang stiger om natten med IR-belysningen; for eksempel er strømindgangen i løbet af dagen 150 mA, mens den om natten er 600 mA. Kameraet bør ikke forsynes med højere spænding for at kompensere for tabet ved strømforsyningskablet, da spændingsfaldet varierer. For et langt strømforsyningskabel med IR-belysningen tændt, vil forsyningsspændingen være tilstrækkelig, men når IR-belysningen er slukket, falder strømindgangen, hvilket øger spændingen ved belastningen, hvilket kan resultere i kameraskader.

Du skal kende modstanden for et enkelt kabelled i Ω/km for at kunne beregne spændingsfaldet. Beregningsmetoderne diskuteres i det næste afsnit. Tabellen viser data for udvalgte tværsnitsområder i leddet.

Eksempel

12 V DC strømforsyning, dobbeltkernekabel, tværsnitsareal 0,5 mm², længde 50 m, kameraindgang (belastning) strømindgang 0,5 A (500 mA). Brug af disse værdier i formlen:

Beregningerne viser, at spændingsfaldet ved tolederkablet er 1,78 V (2 x 0,89 V) - et samlet spændingsfald på tværs af begge leder. Spændingen ved belastningen reduceres til:
12 V - 1,78 V = 10,22 V , som vist i det følgende diagram.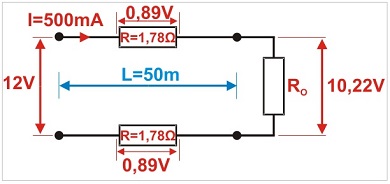

Et procentuelt spændingstab ved strømforsyningskablet kan let beregnes ved hjælp af følgende formel:

hvor:
Ud% - procentuelt spændingstab ved kablet (%),
Ud - spændingsfald,
In - indgangsspænding.

Efter udskiftning af formlen kan det procentuelle spændingstab ved belastningen, dvs. spændingstabet ved strømforsyningsledningen, beregnes.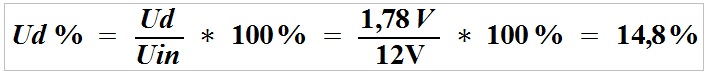

Spændingsfaldet, især ved lav forsyningsspænding, er et alvorligt problem. Med en stigning i forsyningsspændingen vil spændingsfaldet over kablet være det samme, men det procentuelle spændingsfald ved belastningen vil være lavere.

Eksempel

Som i det forrige eksempel: dobbeltkernekabel, tværsnitsareal 0,5 mm², længde 50 m, kamera (belastning) strømindgang 0,5 A (500 mA), 24V DC strømforsyning.

Spændingstab over strømforsyningslinjen: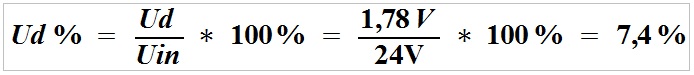

Spændingsfaldet over kablet er 1,78 V , hvilket reducerer spændingen ved belastningen fra 24 V til 22,22V, dvs. med 7,4%, hvilket ikke påvirker belastningen.

Eksempel

Som i de foregående eksempler: tolederkabel, tværsnitsareal 0,5 mm², længde 50 m, kamera (belastning) strømindgang 0,5 A (500 mA), 230 V DC strømforsyning.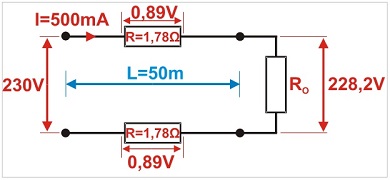

Spændingstab over strømforsyningslinjen: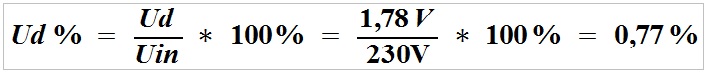

Spændingsfaldet over kablet reducerer 1,78 V og spændingen ved belastningen fra 230 V til 228,2 V, dvs. med 0,77%, hvilket ikke påvirker belastningen.

Lad os analysere tre strømforsyningssager for forskellige spændinger. Spændingsfaldet er i alle tilfælde identisk og påvirkes ikke af forsyningsspændingen. I 230 V-systemer er spændingsfaldet ved belastningen med flere volt ubetydeligt, men i 12 V-system kan spændingsfaldet være et stort problem, hvilket resulterer i forkert funktion af de leverede enheder.

En kendt kabelmodstand i Ω/km kræves til beregninger. Modstanden for et enkelt led beregnes i overensstemmelse med den anden Ohms lov. Det hedder, at modstanden fra en homogen leder med konstant tværsnit er direkte proportional med dens længde og er omvendt proportional med arealet af dets tværsnit.

Det udtrykkes ved en formel til beregning af modstanden af ​​et kabel med længden L og et tværsnitsareal S: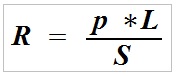

hvor:
R - modstand (modstand) for en enkelt leder udtrykt i ohm (Ω),
p - modstand (specifik modstand) for en leder (Ω mm²/m), der er passende for materialet, som lederen blev lavet (for kobber erstatter vi altid 0,0178 ),
L - lederlængde udtrykt i meter (m),
S - leder tværsnitsareal udtrykt i kvadratmillimeter (mm²).

For kobber er resistiviteten 0,0178 (Ω mm²/m), hvilket betyder, at 1 m af kablet med et tværsnitsareal på 1 mm² har en modstand på 0,0178 Ω (for rent kobber). Det er en grov værdi afhængigt af renheden og de anvendte behandlingsmetoder. For eksempel kan billige kinesisk-fremstillede kabler være lavet af kobber og aluminiumlegeringer eller kan dopes med andre metaller, hvilket øger resistiviteten, modstanden og spændingsfaldet. For aluminium er resistiviteten 0,0278 (Ω mm²/m).

Eksempel

Lad os beregne modstanden af en kobberleder med en længde på 1000 m og et tværsnitsareal på 0,75 mm².

En enkelt leder med en længde på 1000 m har en modstand på 23,73 Ω.

Baseret på ovenstående formel og Ohms lov kan vi nemt beregne den maksimale strøm for en bestemt længde af lederen med et specifikt tværsnitsareal (i mm²). Vi tilføjer 2 til formlen, da vi beregner den faktiske længde på 2 ledere.

Eksempel

For et 30 m langt kabel med et tværsnitsareal på 2 x 0,75 mm²:

Først skal vi bestemme lederens modstand.

For et 12 V-system er spændingsfaldet 1 V, hvilket indikerer, at spændingen ved belastningen er 11 V. Den maksimale strøm kan beregnes ud fra Ohms lov.

Eksempel

Et parsnoet kabel har 4 ledere. Vi beregner et spændingsfald over et enkelt ledningspar ved en belastnings strømindgang på 500 mA (0,5 A) til et 40 m langt UTP K5 parsnoet kabel med et tværsnitsareal på 0,19625 mm² tilsluttet et 12 V-system.

Vi beregner lederens modstand (UTP K5 parsnoet kabel har et tværsnitsareal på 0,19625 mm²):

Ved hjælp af Ohms lov beregner vi et samlet spændingsfald på tværs af to kerner ved 500 mA (0,5 A) strømindgang.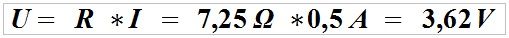

Dvs. spændingsfaldet ved forsyningsledningen er 3,62 V, og spændingen ved belastningen er 8,38 V (12 V - 3,62 V = 8,38 V).

Den maksimale strøm for spændingsfaldet på 1 V for et 12 V-system kan også beregnes ved hjælp af Ohms lovligning, hvor spændingen ved belastningen reduceres til 11 V.

Beregningerne blev foretaget for et enkelt parsnoet kabel. 2, 3 eller 4 par af det parsnoet kabel bruges ofte til at reducere spændingsfaldet. Parret er forbundet parallelt for at øge tværsnitsarealet og reducere linjemodstanden, hvilket resulterer i lavere spændingstab.

Beregningerne for de samme parametre: UTP K5 parsnoet kabel, strømindgang 500 mA (0,5 A), længde 30 m længde, strømforsyning 12 V:

Tabellen viser den maksimale strøm, der kan overføres af kablet med en bestemt længde og et tværsnitsareal, hvor spændingsfaldet ved belastningen ikke overstiger 1 V. Beregningerne blev foretaget for to kabelledere.

Den næste tabel viser den maksimale strøm, der transmitteres af det snoede par-kabel af en bestemt længde, hvor spændingsfaldet ved belastningen ikke overstiger 1 V. Beregningerne blev udført for den effekt, der blev transmitteret gennem 1, 2, 3 og 4 par det snoede par kabel (kat. 5 og 6).

Et leders tværsnitsareal i kvadratmillimeter skal være kendt. Denne parameter er ikke den samme som diameteren.

For tykkere kabler, såsom strømkabler, giver producenter og distributører tværsnittet i kvadratmillimeter (mm²). For tyndere kabler, f.eks. telekommunikations-og it-kabler, er kabeldiameteren angivet i millimeter (mm), og i disse tilfælde skal vi konvertere diameteren til tværsnittet.

Diagrammet viser forskellen mellem kabeldiameteren og tværsnitsarealet: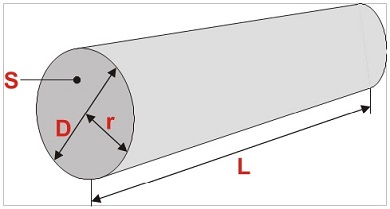

hvor:
S - kabelens tværsnitsareal i kvadratmillimeter (mm²),
D - kabeldiameter i millimeter (mm),
r - kabelradius (halvdelen af dens diameter) i millimeter (mm),
L - kabellængde.

Tværsnitets areal:

eller

π - en matematisk konstant = 3,14

Eksempel

Kat. 5e UTP. Diameter angivet af producenten er 0,5 mm. Vi skal beregne tværsnitsarealet i mm².

eller

Et kabel med diameteren 0,5 mm har et tværsnitsareal på 0,19625 mm².

Resumé

De vigtigste faktorer, som påvirker spændingsfaldet: